Line Segment Intersection

Problem definition: Given n lines S1, S2, ...., Sn defined by points (p1, q1), (p2, q2), ...., (pn, qn) in 2D Euclidean space the goal is to compute all intersection points i_jk where j and k ranges from 1 to n and j ≠ k.

In Introduction we have defined how to compute the point of intersection for two line segments intersect. It takes O(1) time to compute the intersecting point. In this section we are going to deal with the problem computing all the intersection points for arbitrary number of segments.

The brute-force way to find the intersection points is to compute them for every pair. This would take O(n²) time. Below, we describe the plane-sweep algorithm that works in O((n+k)logn) where k is the number of intersection points.

Plane-sweep algorithm

The intersection points can be computed using a vertical line L that sweeps through the 2D plane from left-to- right (or equivalently with a horizontal line that sweeps from top to bottom). We will not focus on the sweeping line at every point in the x-axis. Instead, we will restrict our attention to just few points, which we call as event points. These event points include the start and end points of each segment, pi's and qi's which are known at the beginning, plus the points of intersection i_jk's, which are computed dynamically while the vertical line sweeps through the space.

Towards this end, we have to maintain a data structure EVENTS that contains the event points sorted based on the x-coordinate. Note that initially, EVENTS will consist only initial and end points (pi's and qi's) of the segments. As it stops at each of these points, intersecting points will be computed dynamically and added to EVENTS. A priority queue serves as a good data structure to keep EVENTS sorted as the intersection points are added.

We know that n segments imply 2n end points while the number of intersecting points k may vary. At one extreme, none of the lines may intersect which implies k = 0. At another extreme, every line may intersect with the other, in which case, k = 1 + 2 + ... + n-1 = O(n²) points of intersection. The following figure shows both these cases.

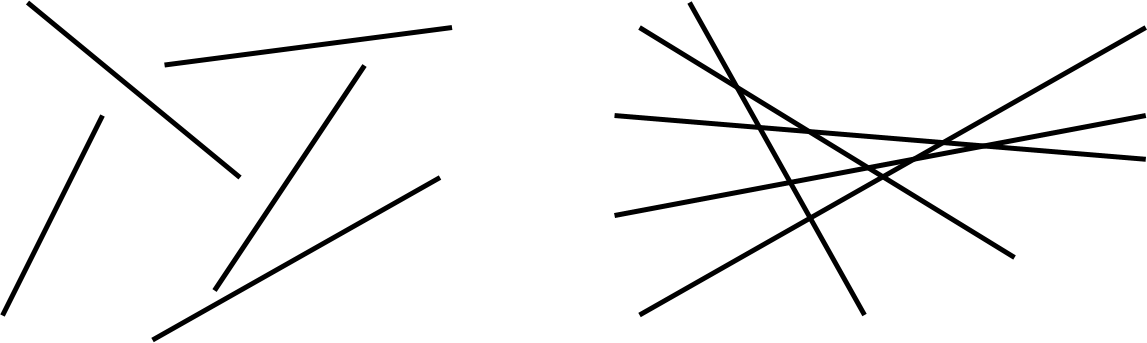
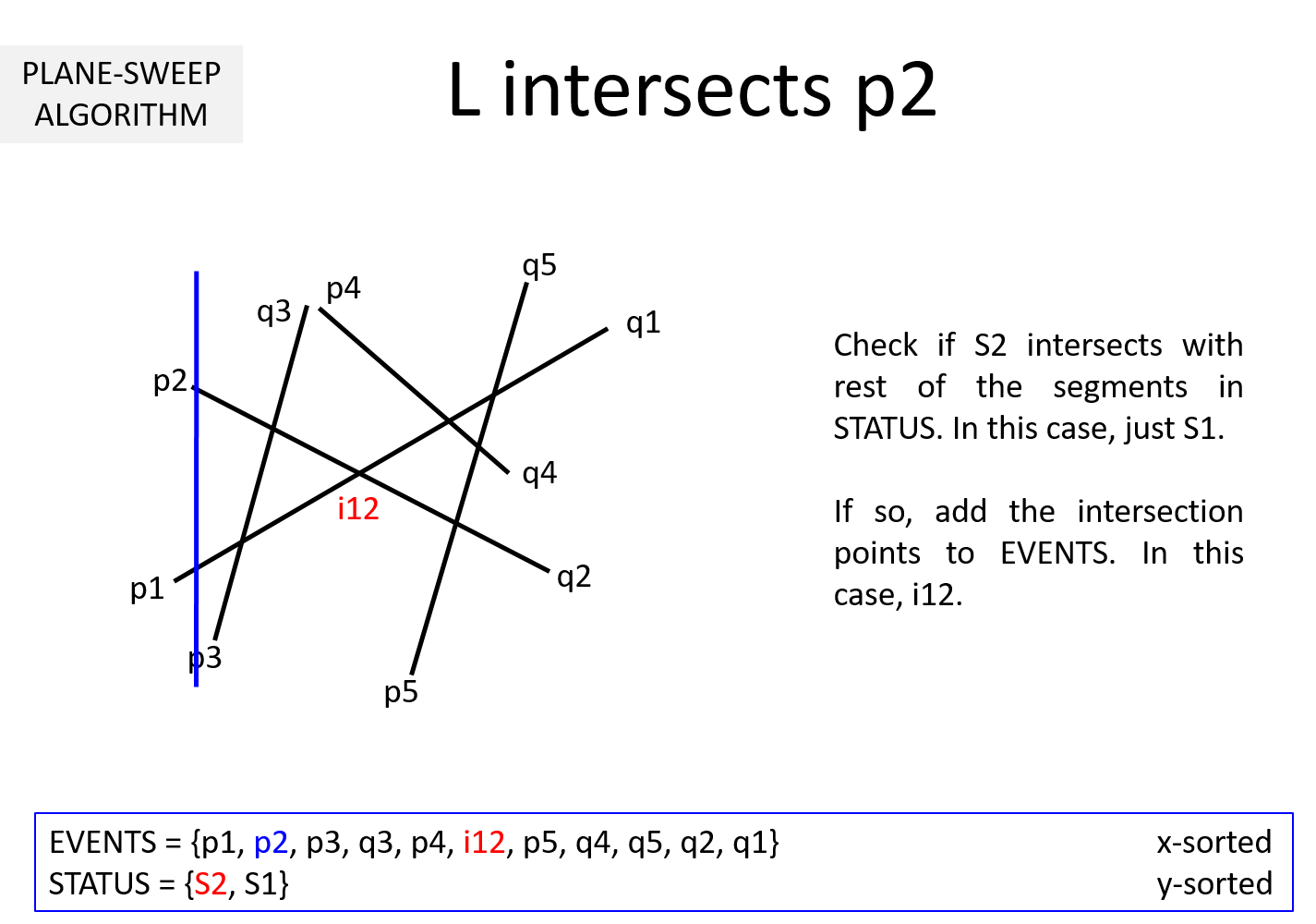
To start with, the vertical line L is at the left extreme of the line segments as shown below. Then on, it will stop at the event points pi's, qi's and i_jk's where i_jk denotes the intersection point of Sj = (pj, qj) and Sk = (pk, qk).

As it stops at each of these points, it will compute the intersecting points i_jk's dynamically and add them to EVENTS.

Question 1: How do we know when to compute intersection between segments?

The moment sweepline L has seen the initial point pi of more than one segment, we have to compute their intersection. Towards this end, we maintain a data structure STATUS, to keep track of the segments Si's, whose initial points we have seen thus far. As the initial point of a new segment Sk is encountered, we compute the intersection of Sk with all the active segments in the STATUS data structure, add the intersection points to EVENTS and finally add Sk to the STATUS.

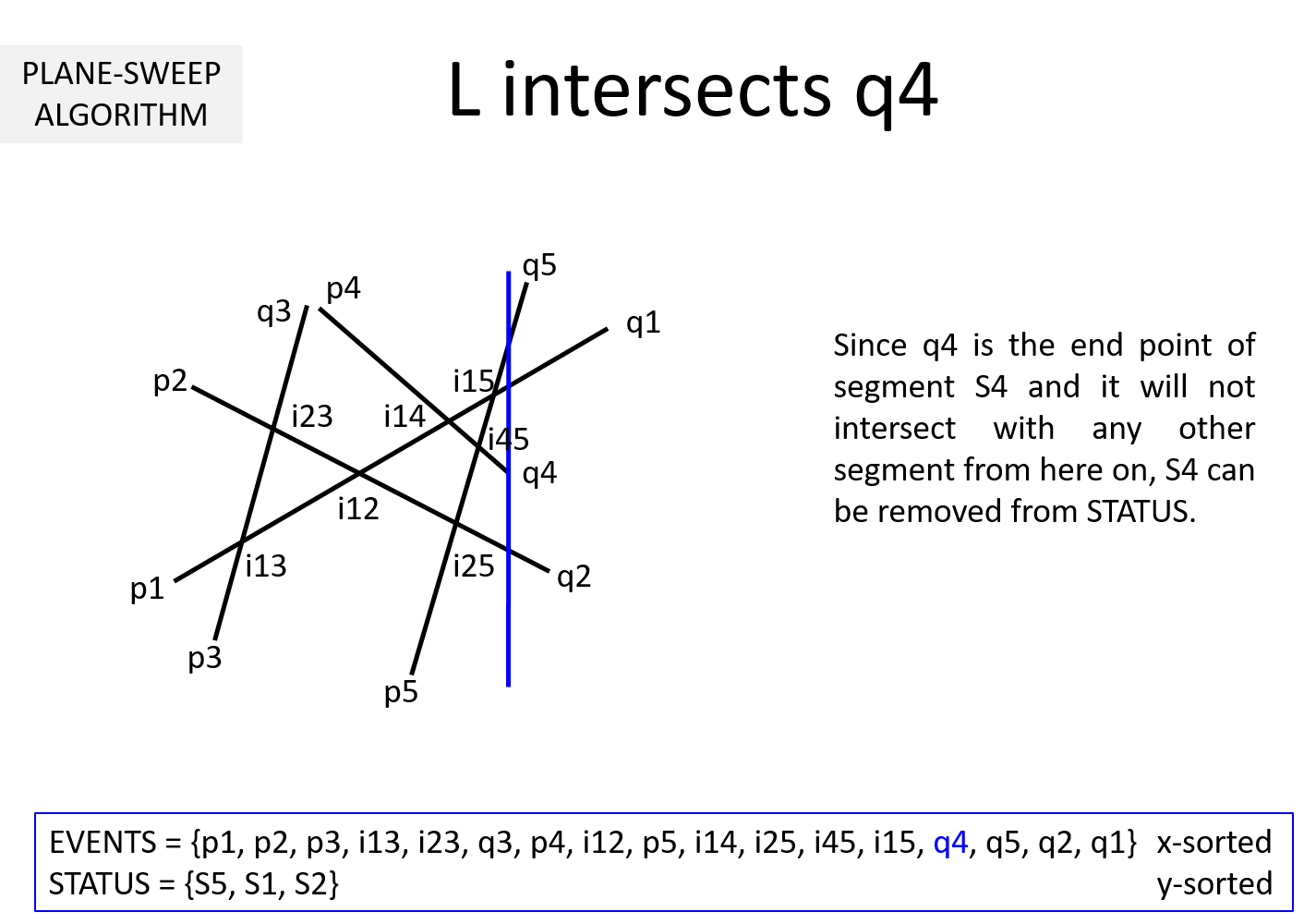
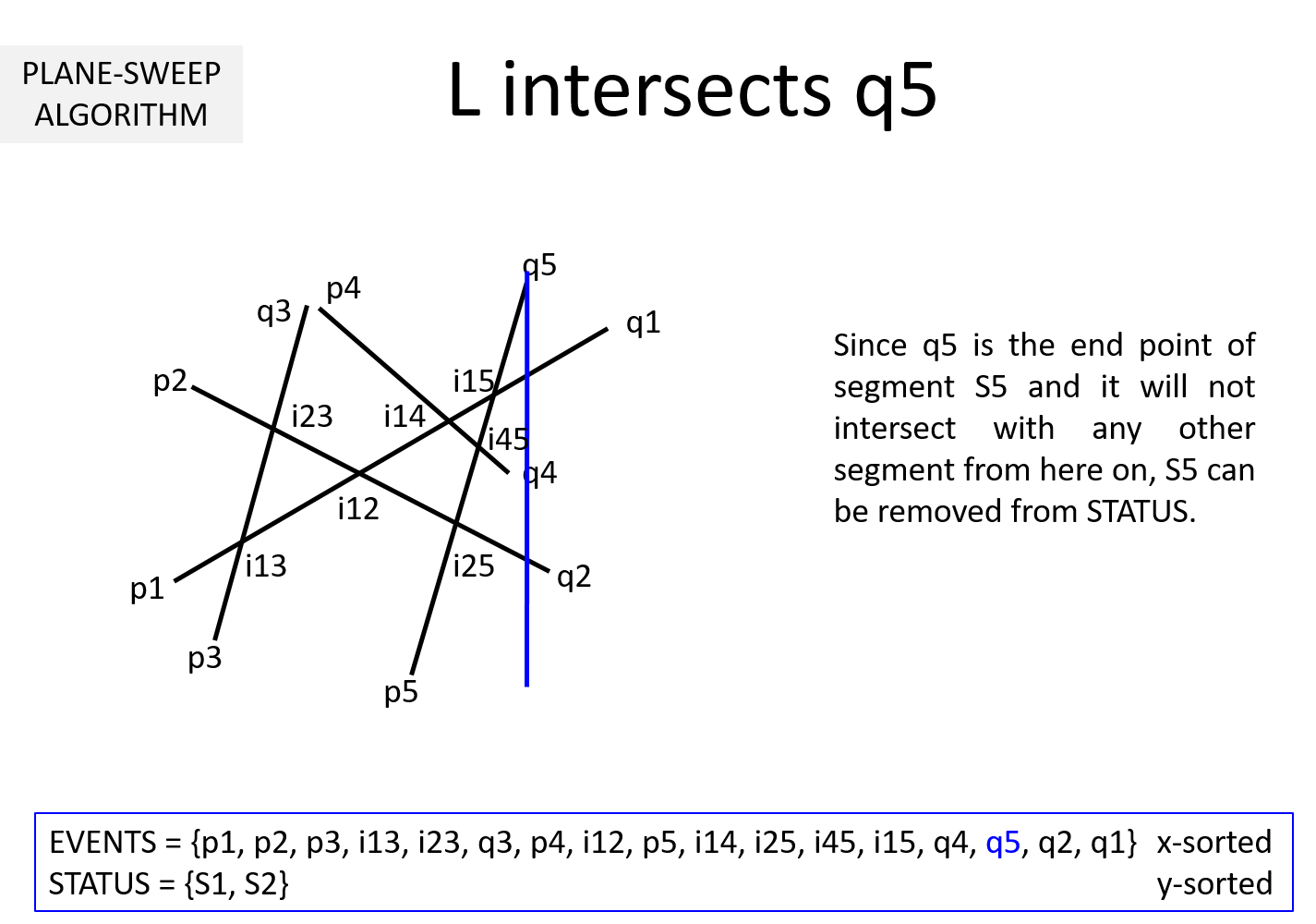
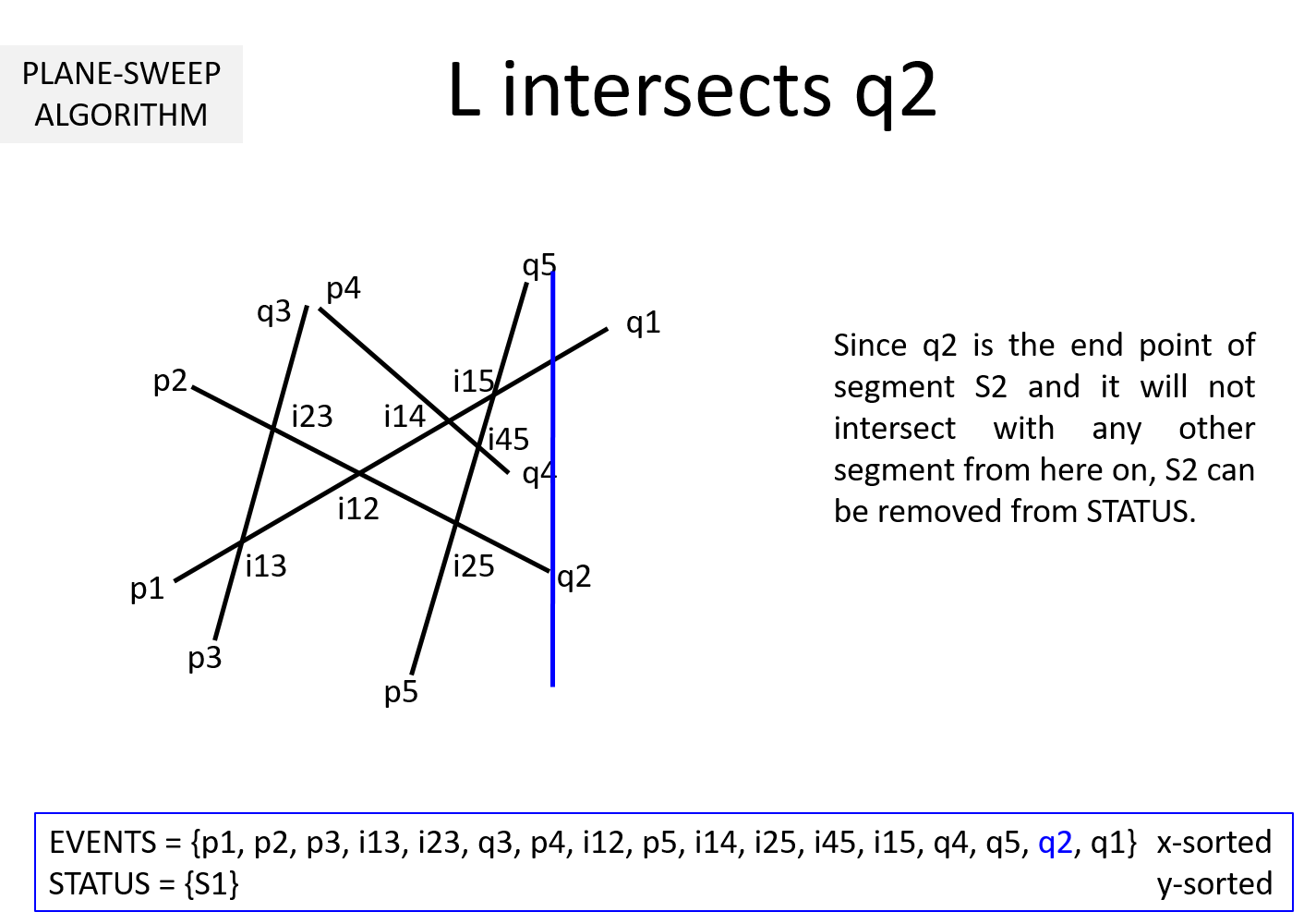
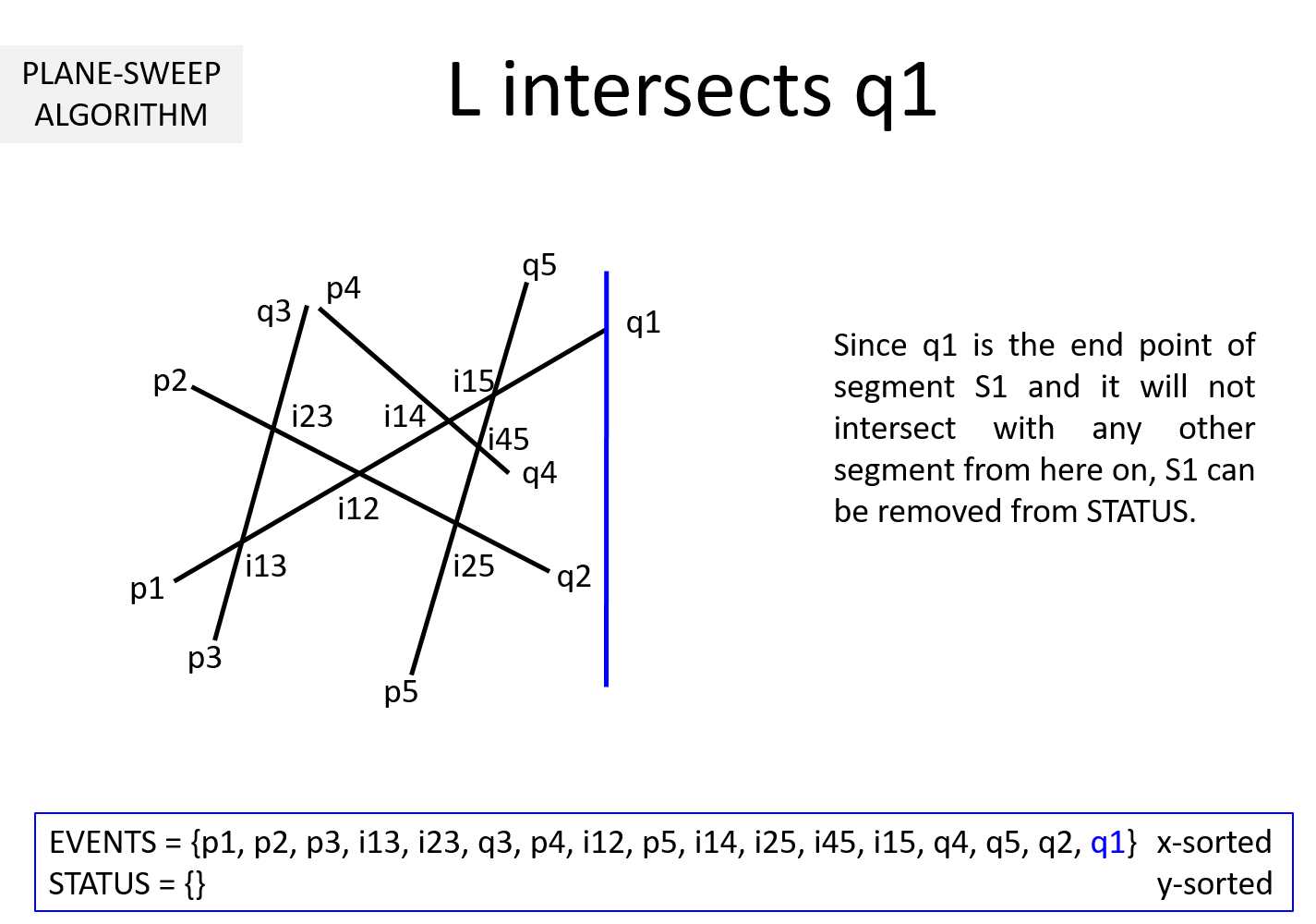
Question 2: What if the sweepline goes past the end point qi of a segment Si?

Then the segment Si cannot intersect with any segment henceforth. So, Si can be removed from STATUS.

We will demonstrate the algorithm using an example first. Consider the following figure consisting of five line-segments (p1, q1), ...., (p5, q5). The initial position of the sweep-line L is shown below. The STATUS is empty and EVENTS contains only pi's and qi's sorted based on x-coordinate.

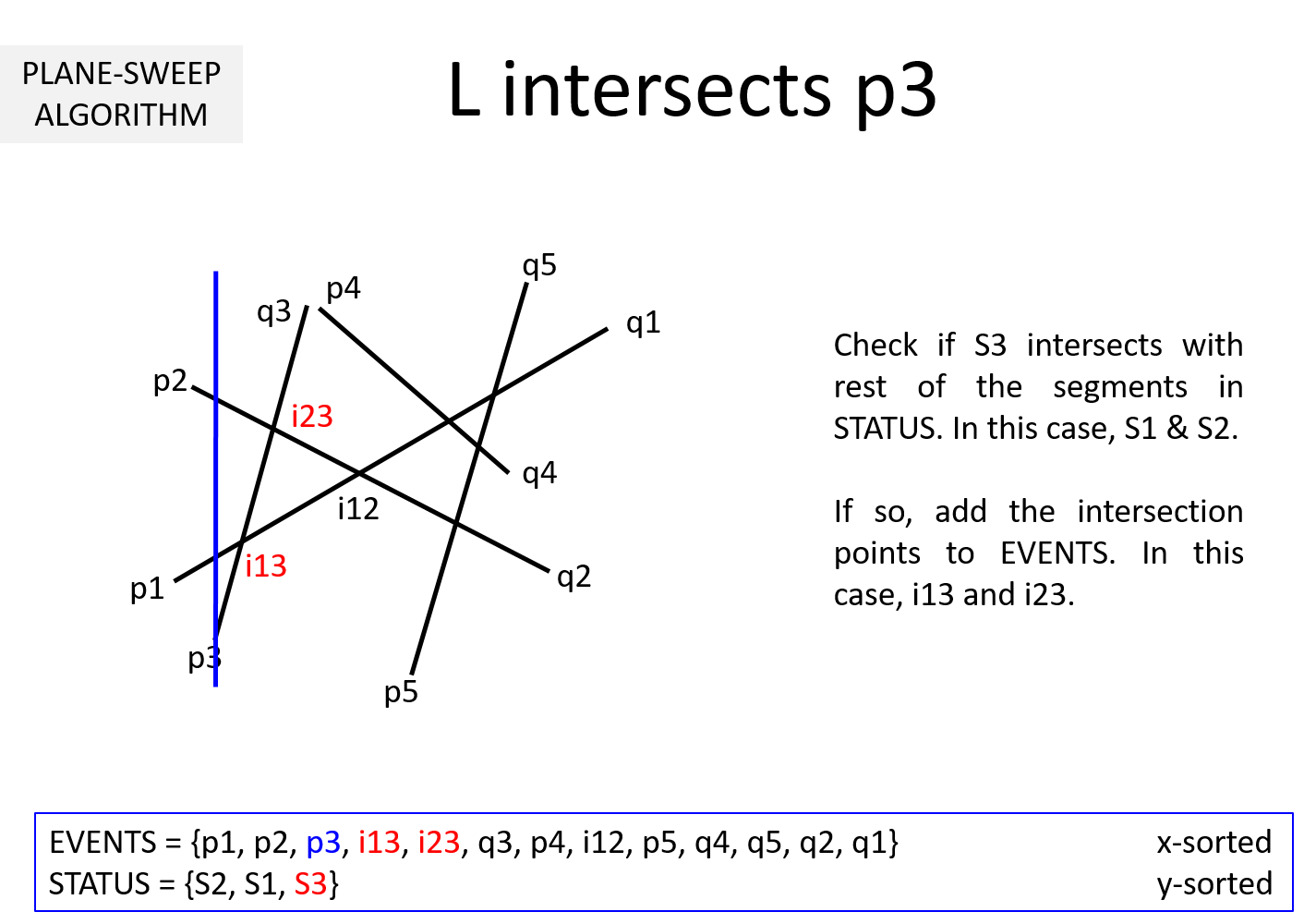
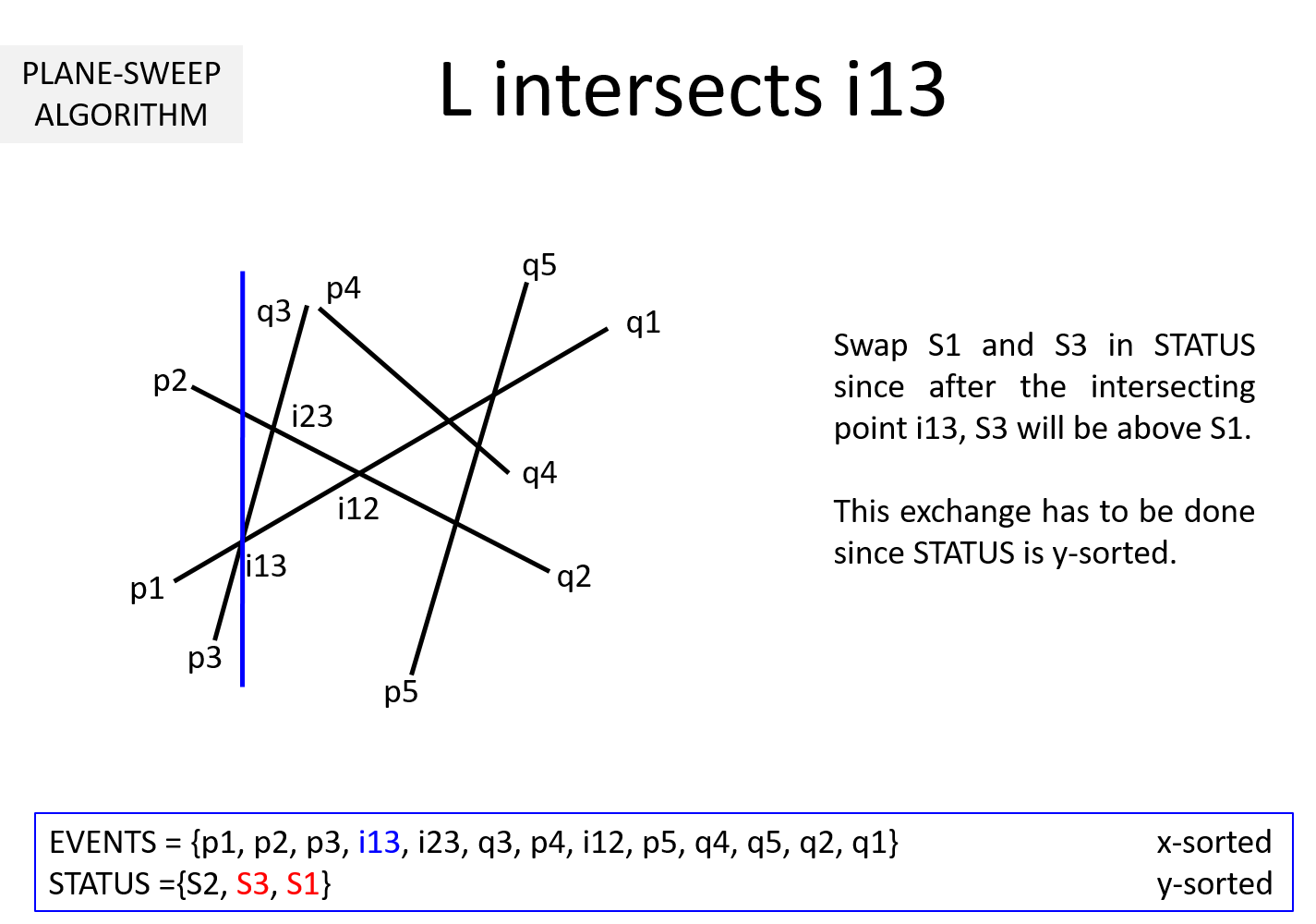
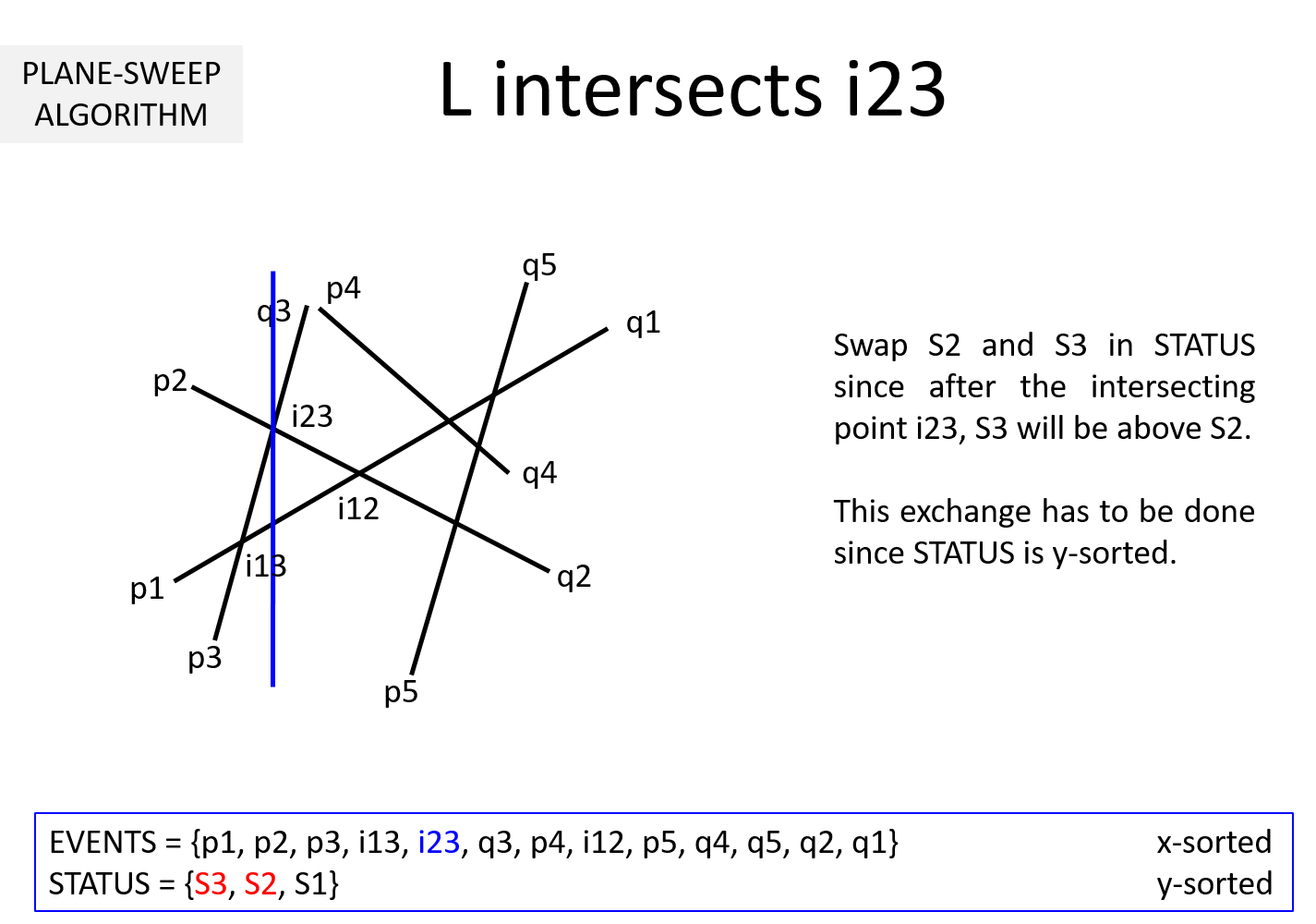
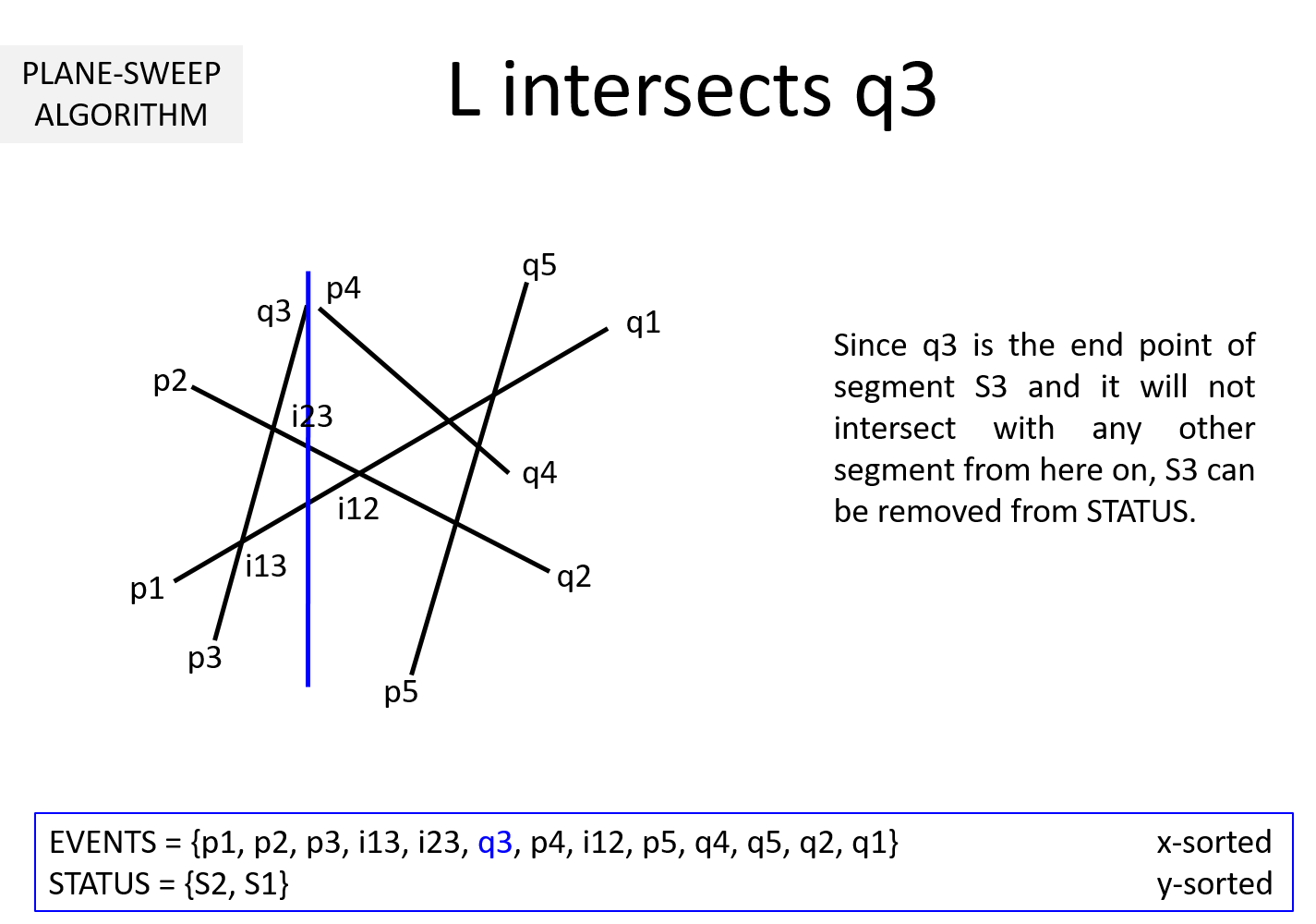
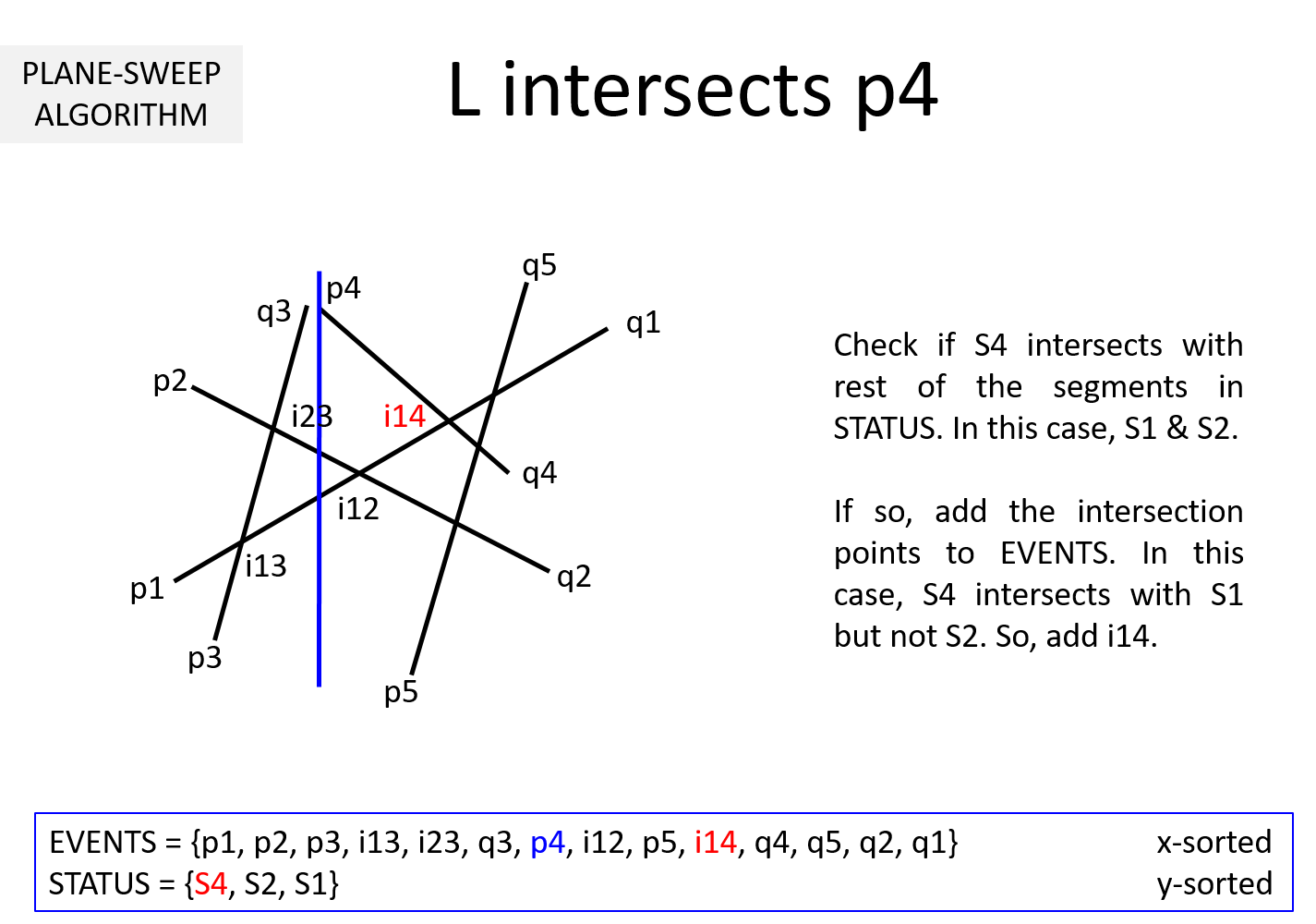
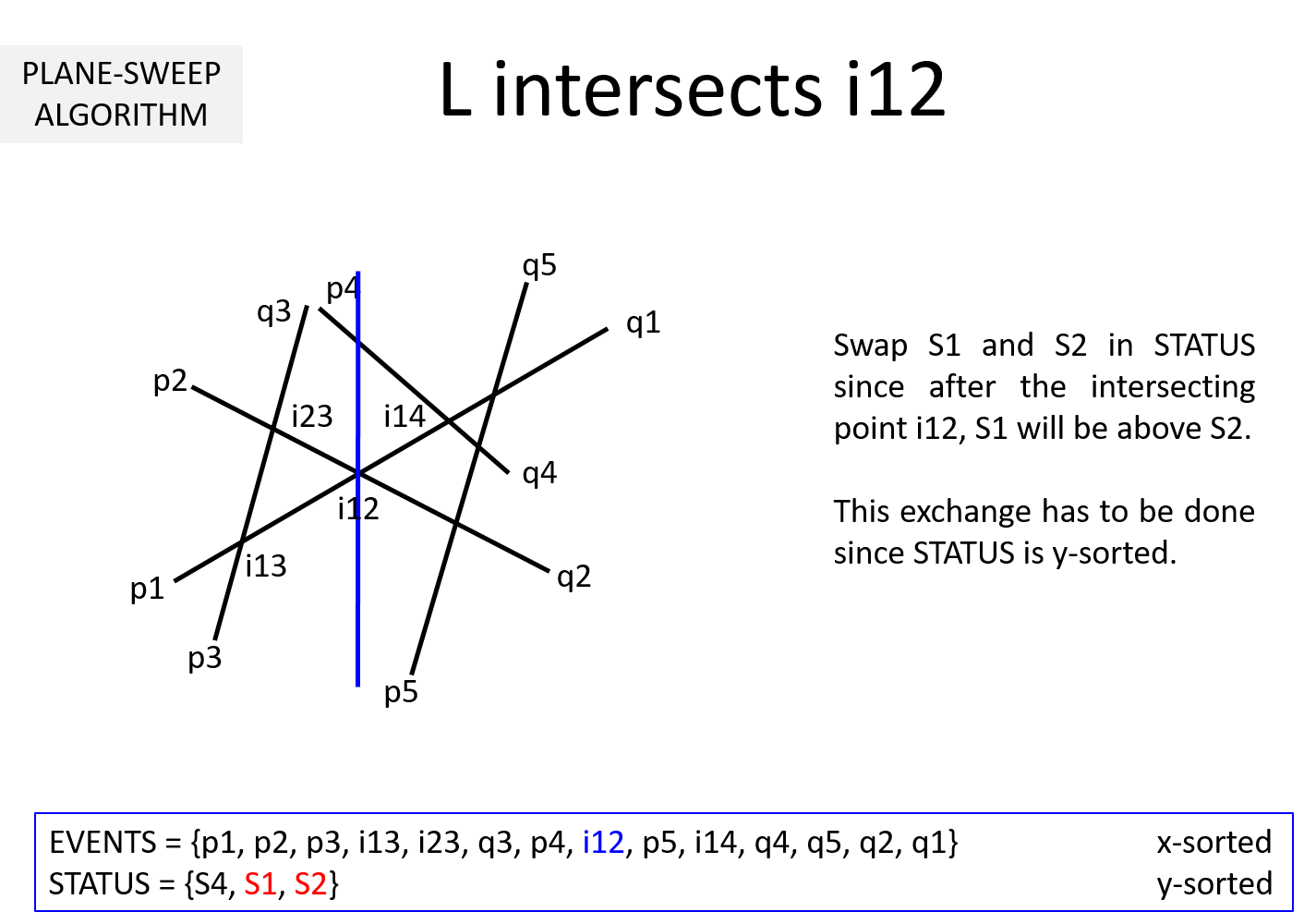
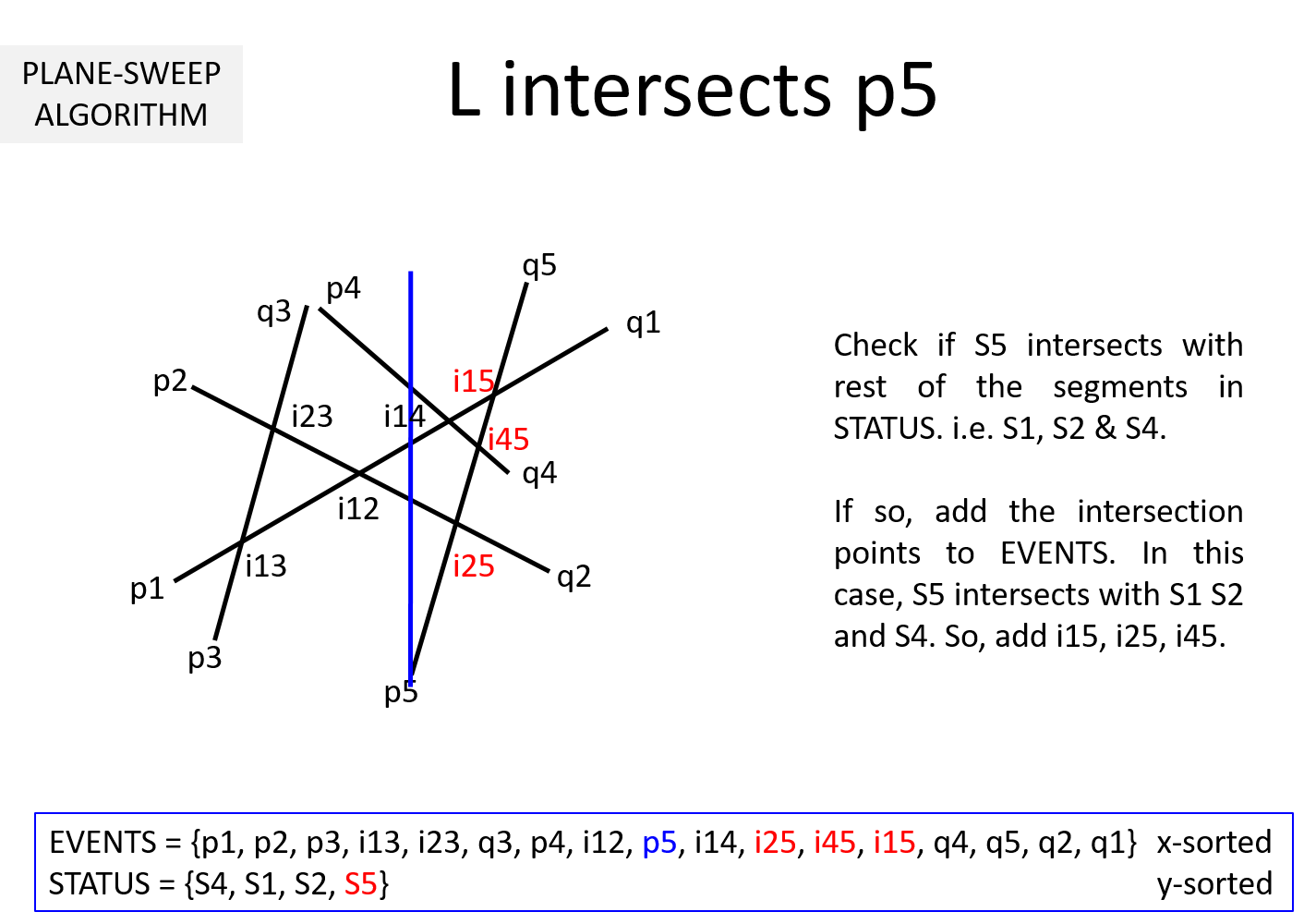
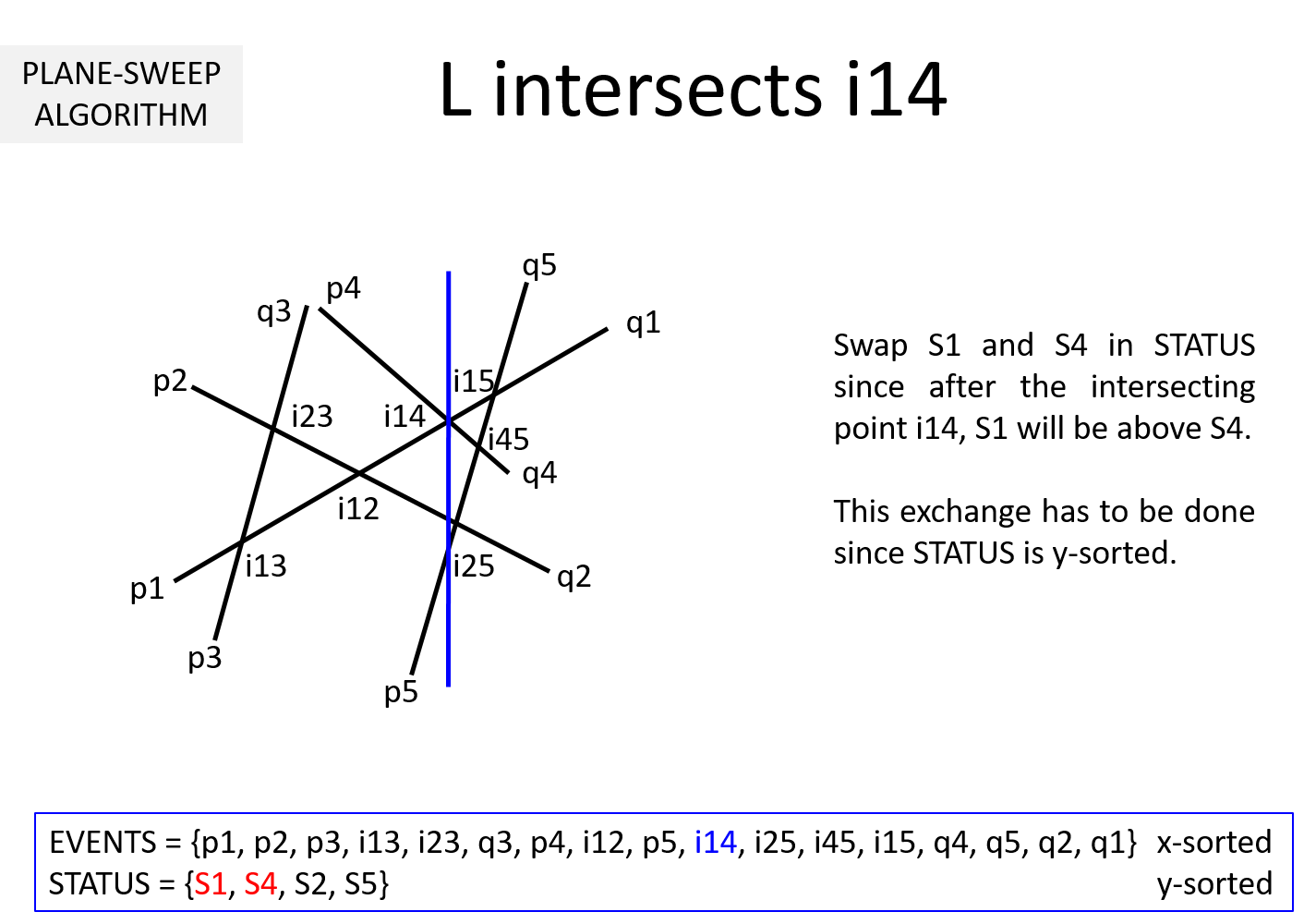
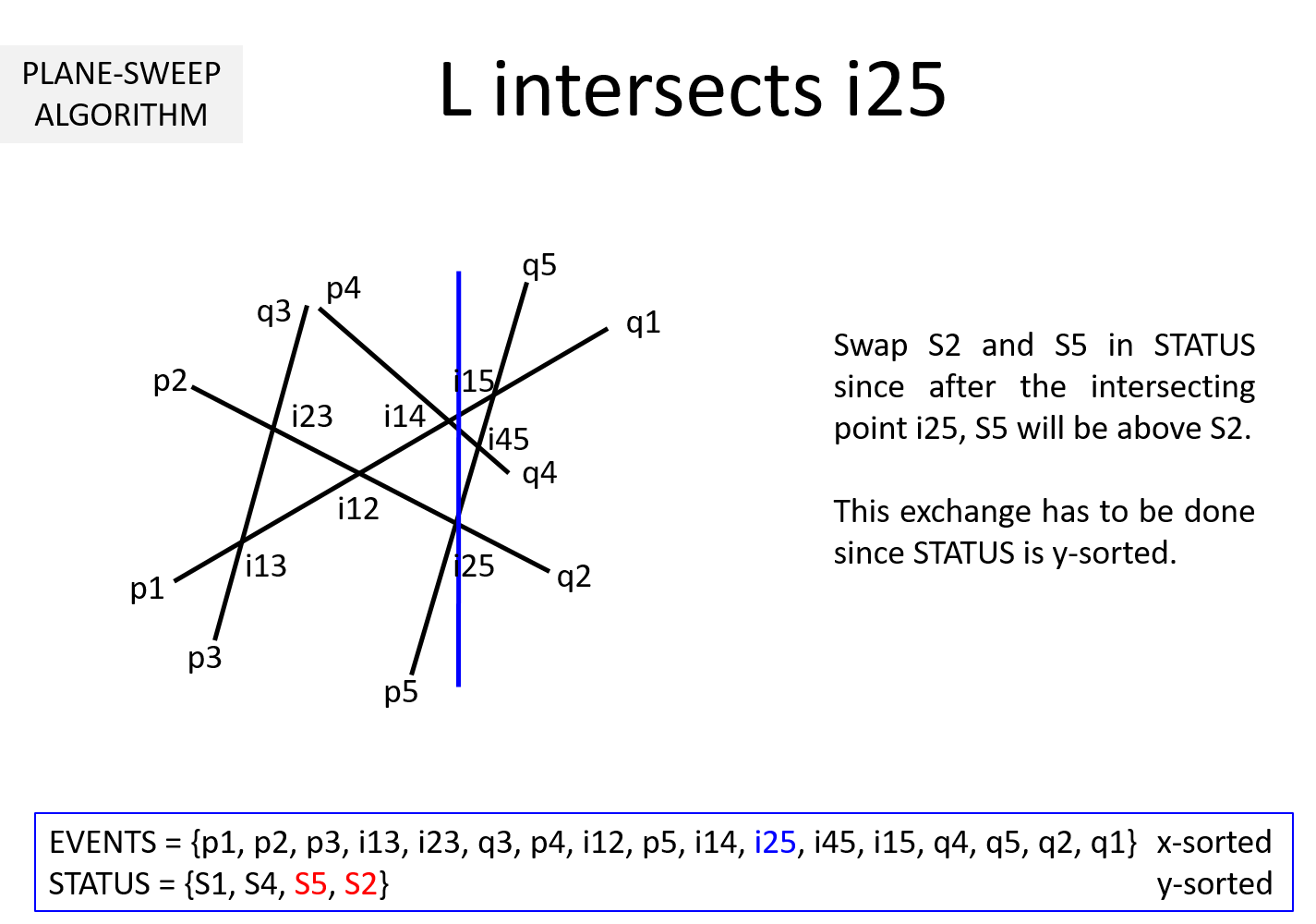
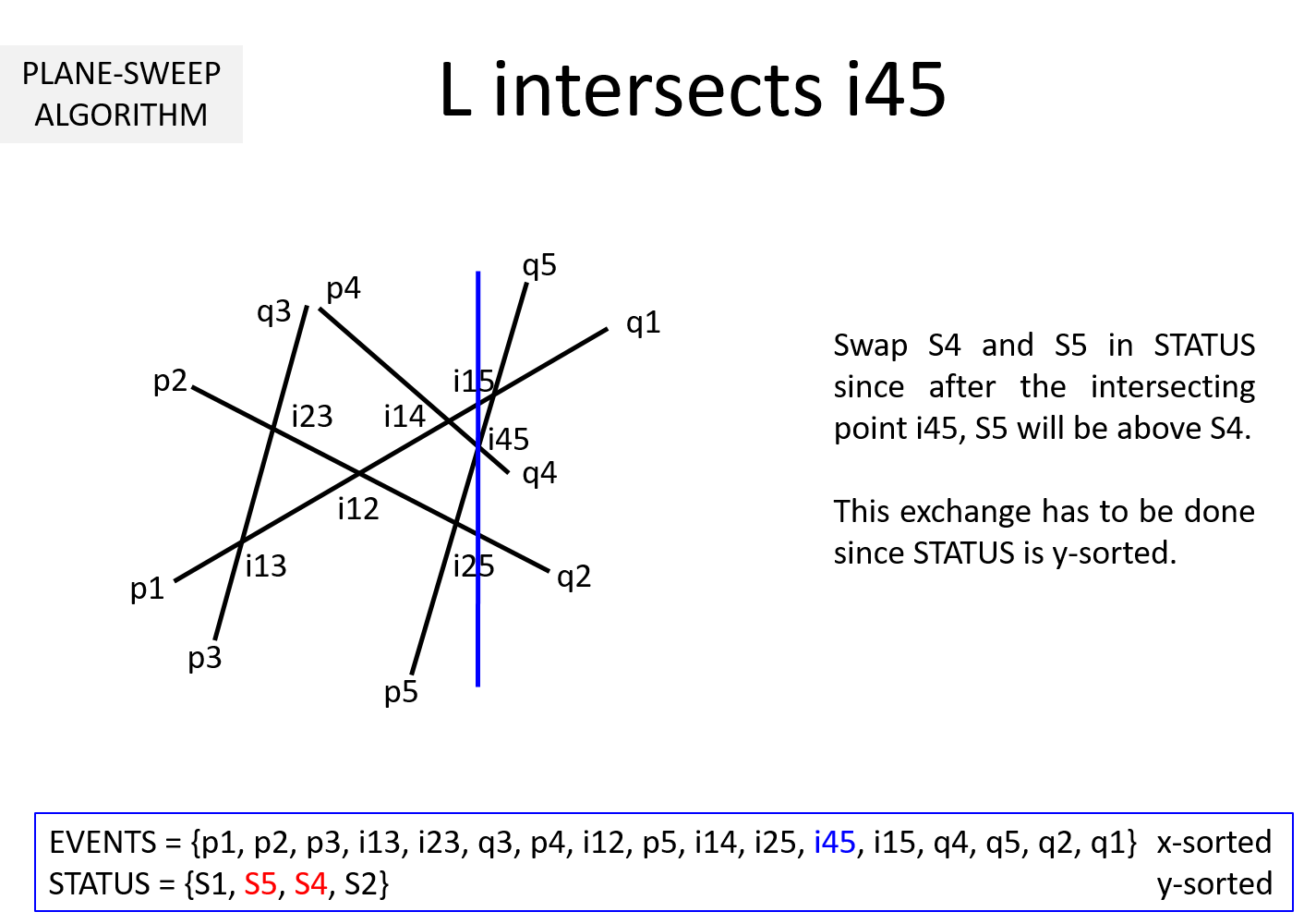
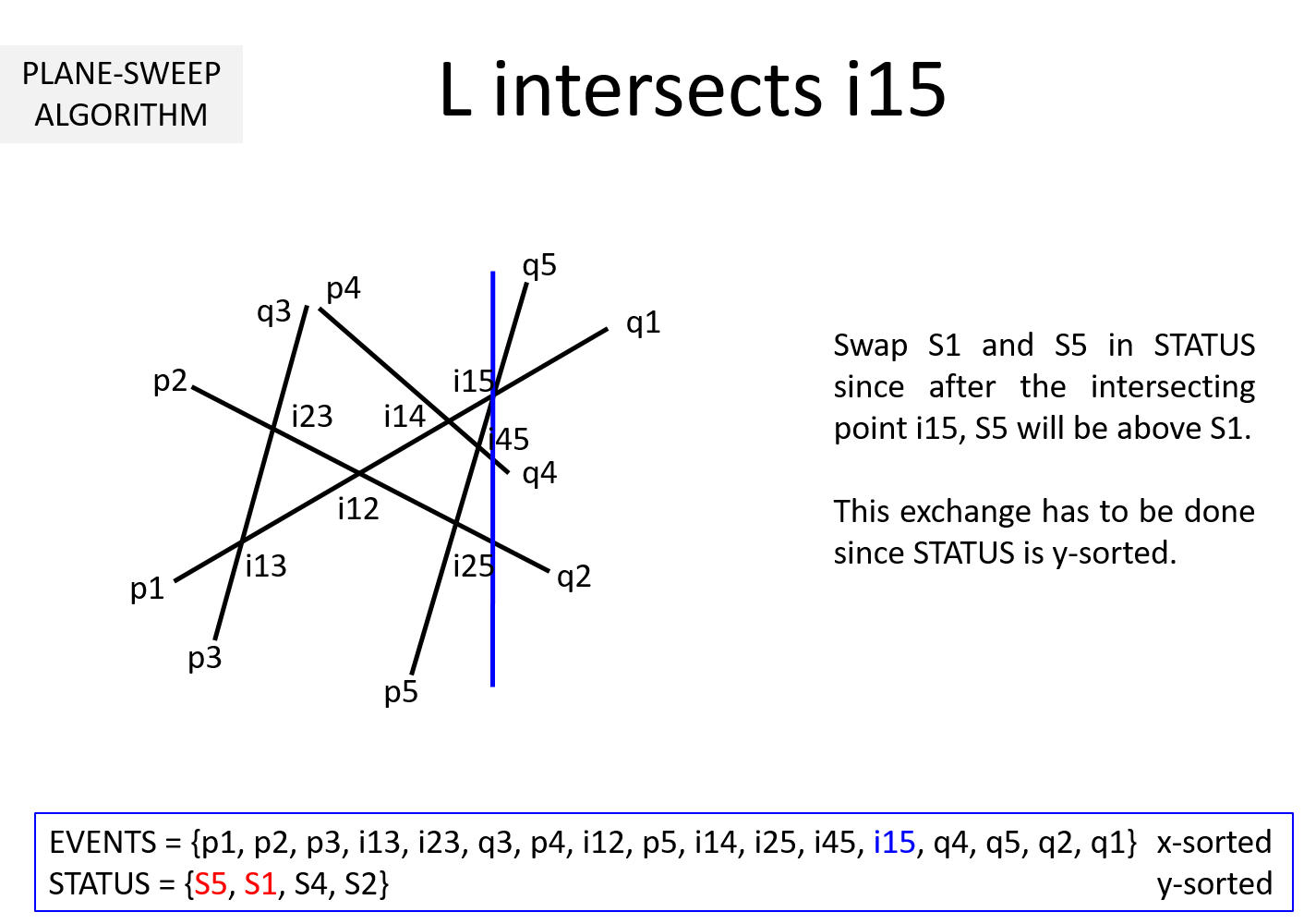
Question 3: It is clear from the above example that EVENTS must be maintained in a sorted manner so as to sweep from left to right. But, why should STATUS be kept sorted (per y-coordinate)? In the above example, we noted that while the sweepline L is at an intersection i_jk, we exchange Sj and Sk to keep STATUS sorted. Why is it necessary?

It turns out that maintaining STATUS in sorted manner helps in optimizing the algorithm. Whenever L hits a start point pi of a segment Si, we immediately compute the intersection points of Si with all the segments in STATUS. This takes O(n) time. This repeated for n segments leads to O(n²) intersection computations. To be precise, 0 + 1 + 2 + .... + n-1 computations are needed at worst.

If we keep STATUS sorted, at each pi it is sufficient to compute the intersection point of Si with its upper Su and lower segment Sl. This takes O(1) time. The remaining computations can be moved to when L hits the intersection points. When L hits i_jk, Sj and Sk are swapped leading to Sj and Sk getting a new neighbor (upper neighbor of one and lower neighbor for the other).

Without loss of generality, lets assume Sj is above Sk before intersection and STATUS = {..., Sx, Sj, Sk, Sy, ...}. After L hits S_jk, STATUS = {..., Sx, Sk, Sj, Sy, ...}. Sk's new neighbor is Sx and Sj's new neighbor is Sy. Two computations are necessary to determine intersection point of Sx-Sk and Sj-Sy. This works out to O(1) time.

To sum up, at each pi, 2 intersection computations are done and at each i_jk again, 2 intersection computations are done. Thus, the overall intersection computations reduces to O(n + k) instead of O(n²).

Question 4: What would be an appropriate data structure for STATUS?

Priority queue does not suit since we not only need to keep it sorted, but have to find the upper and lower neighbor of segment whenever the sweeping line hits the starting points pi's and intersection points i_jk's. A 2-3 tree serves as an appropriate data structure. Look into Chapter 2.3 of Computational Geometry - Methods and Applications

Algorithm: Plane-sweep

// Input: n segments S1, ..., Sn
// Output: All intersection points of these segments

DECLARE PriorityQueue EVENTS // Sorted by x coordinate left-to-right
DECLARE TwoThreeTree STATUS // Sorted by y-coordinate top-to-bottom
Include end points of S1, ..., Sn to EVENTS
STATUS = {}

for (i = 1; i < EVENTS.length; i++) {
	Point p = EVENTS[i]
	if ( p = left-end of a segment S )
		Let Sj and Sk be the neighboring segments to S
		Point q = Intersection(S, Sj)
		Point r = Intersection(S, Sk)
		if (q != null) 
			OUTPUT q
			EVENTS = EVENTS ∪ {q}
		if (r != null) 
			OUTPUT r
			EVENTS = EVENTS ∪ {r}
		STATUS = STATUS ∪ {S}
	else if ( p = intersecting point of Sj and Sk)
		Swap Sj and Sk in STATUS
		Let Sx be the new neighbor of Sj
		Let Sy be the new neighbor of Sk
		Point q = Intersection(Sx, Sj)
		Point r = Intersection(Sk, Sy)
		if (q != null) 
			OUTPUT q
			EVENTS = EVENTS ∪ {q}
		if (r != null) 
			OUTPUT r
			EVENTS = EVENTS ∪ {r}
	else if ( p = right-end of a segment S)
		Remove S from STATUS;
}

Complexity

The loop runs for (n + k) times where n is the number of segments and k is the number of intersection points. Within the loop, computation of intersections twice takes O(1) time while insertion of the intersection points take O(log n) time. Thus the overall complexity is O((n+k)logn).

Corner cases

There are several corner cases when algorithm might fail. Think how will you handle these cases. How should you change the algorithm to deal with such cases?

An end point of a segment barely touches another segment.
An end point of a segment barely touches the end point of another segment.
A segment is parallel to y-axis.
Three or more segments intersect at the same point.
Floating point calculations can lead to declaring a non-intersecting point as intersecting and vice-versa. This is a real challenge in geometric algorithms.

Computational Geometry