| Prev | Next |
Deterministic Finite State Automata
A deterministic finite state automaton is a 5-tuple (Q, Σ, δ, q0, F) where
- Q denotes the finite set of states
- Σ represents the alphabet that consists of input symbols
- δ: Q x Σ = Q denotes the transition function the defines the transition from qi ∈ Q to qj ∈ Q for each input symbol.
- q0 denotes the start state
- F denotes the set of final states
Given an input sequence, the DFA processes the string of symbols one at a time, moves between the states as defined by the transition function δ. The string is said to be accepted by the DFA, if at the end of the processing, the final state is reached. In a DFA, there is exactly one transition from one state to another for each input symbol.
It is easier to catch the idea of a DFA with examples. We will start with some really simple ones and progressively do tougher ones.
1. DFA that accepts exactly one a. Σ = {a}
Since the alphabet consists of only a, we need to construct a DFA which accepts only the string "a".
We start with the initial state q0, once we read an a, move to the final state q1.
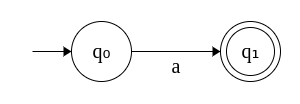
Note that we haven't defined any transtion from q1. This implies that if any input symbol is read, we move to a dead state - meaning the string will never be accepted. For example, if a input string is "aa", it will not be accepted by the DFA.
Alternately, we can also choose to draw the below DFA with an explicit dead state q2.
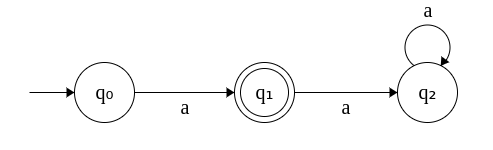
2. DFA that accepts at least one a. Σ = {a}
This is similar to the previous case except that we now have a self-loop at q1 that denotes we remain in the final state henceforth upon reading any number of ways. Thus, this DFA accepts strings "a", "aa", "aaa", ..... Note that the acceptable strings are infinite.
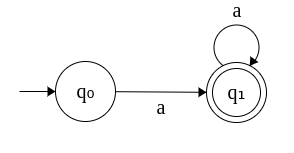
3. DFA that accepts at most one a. Σ = {a}
This implies the DFA can accept exactly two strings: ε and "a". Note that ε denotes the 0-length string. This is similar to the first problem with a single change: the initial state q0 is final too.
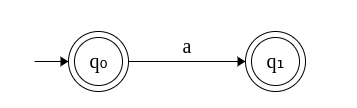
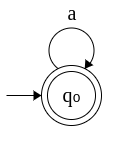
4. DFA that accepts any number of a's. Σ = {a}
The DFA should accept zero or more a's. i.e. ε, a, aa, aaa, .... The DFA is given below. Note that we do not need two states now.
5. DFA that accepts exactly two a's. Σ = {a}
The DFA accepts the only string"aa".

Exercise: Try drawing DFAs for accepting at least 2 a's, at most 2 a's, 5 a's.
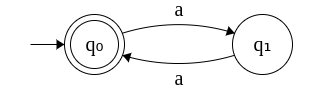
6. DFA that accepts even number of a's. Σ = {a}
The DFA accepts the strings ε aa, aaaa, aaaaaa, ....
Exercise: Try drawing DFAs that accepts strings with odd number of a's
Next, we look at two corner cases. A DFA that accepts anything and a DFA that rejects anything.
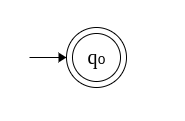
7. DFA that accepts anything. Σ = {a}
This DFA is in final state without having to read any input.
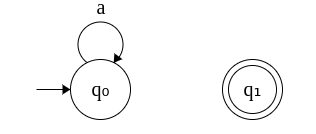
8. DFA that accepts nothing. Σ = {a}
This DFA does not have a transition to the final state which implies there is no way to get there. So, no matter what the input string is, it will be rejected.
Now, lets include one more symbol to the alphabet. Σ = {a, b}.
9. DFA that accepts strings with exactly one a. Σ = {a, b}
The DFA accepts strings such as a, ab, abb, abbb...., ba, bba, bbba, ...., bab, bbab, babb, .... and reject strings that contain no a's or more than one a's.
Step 1: We first draw the basic DFA that accepts a.

Step 2: Next we examine, for each state, what transition to make if symbol 'b' is read.
- q0 denotes the initial state where we have not seen an 'a' so far. So, we can remain in the same state.
- q1 denotes the final state where we have seen exactly one 'a'. So, we can remain in q1.
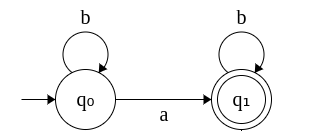
Note: We haven't defined any transition from q1 for input symbol 'a'. This implies, if 'a' is encountered we move to a dead state.
10. DFA that accepts strings with at least one a. Σ = {a, b}
The DFA accepts strings with all combinations of a's and b's so long it has at least one a. In other words, it will reject all strings that are made of only b's (b, bb, bbb, ....).
Step 1: We first draw the basic DFA that accepts a.

Step 2: Next we examine, for each state, what transition to make if symbol 'b' is read.
- q0 denotes the initial state where we have not seen an 'a' so far. So, we can remain in the same state.
- q1 denotes the final state where we have seen one 'a'. So, we can remain in q1.
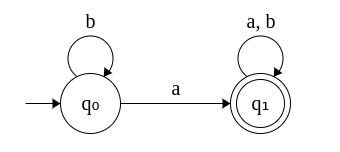
Exercises: Draw DFAs for problems 3, 4, 5, 6, 7 and 8 in a similar vein with Σ = {a, b}.
11. DFA that accepts strings with at least two a's and one b. Σ = {a, b}
Since the a's and b's can appear in any order in the input, the DFA can be given as follows.
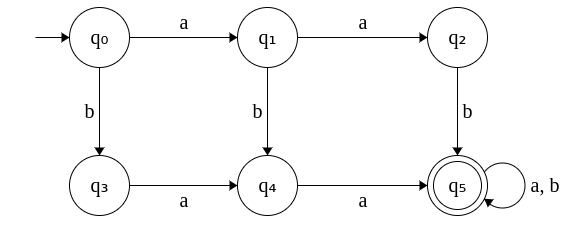
12. DFA that accepts even number of a's and odd number of b's. Σ = {a, b}
Hint: The DFA can be consolidated into four states.
- Even number of a's, even number of b's (say q0)
- Even number of a's, odd number of b's (say q1)
- Odd number of a's, even number of b's (say q2)
- Odd number of a's, odd number of b's (say q3)
q1 must be the final state. First, try on your own. Check here for answer.
Exercise: Draw DFA that accepts either even number of a's and b's OR odd number of a's and b's.
13. DFA that accepts strings that starts with a. Σ = {a, b}
Try on your own first. Check here for answer.
14. DFA that accepts strings that ends with a. Σ = {a, b}
Try on your own first. Check here for answer.
15. DFA that accepts strings that starts and ends with a. Σ = {a, b}
Try on your own first. Check here for partial answer which you can enhance OR here for complete answer.
16. DFA that accepts strings that starts with a and ends with b. Σ = {a, b}
Try on your own first. Check here for partial answer which you can enhance OR here for complete answer.
17. DFA that accepts strings that start and end with same symbol. Σ = {a, b}
The DFA should accept strings that starts and ends with 'a' OR starts and ends with b.
This is left as an exercise.
18. DFA that accepts strings that start and end with different symbols. Σ = {a, b}
The DFA should accept strings that starts with 'a' and ends with 'b' OR starts with 'b' and ends with 'a'.
This is left as an exercise.
19. DFA that accepts strings that ends with abb. Σ = {a, b}
Step 1: Draw the DFA for the basic string abb.

Step 2: Draw out remaining transitions from each state.
Try on your own first. In case you aren't sure, check out for the hint below. Decide the transitions appropriately. You don't need to add any new states!
- At q0, if you encounter 'b', you need too look for the whole pattern "abb".
- At q1, if you encounter 'a' again, you just need to look for "bb" to end with.
- At q2, if you encounter 'a', you need to look for "bb" again to end with.
- At q3, you may encounter 'a' or 'b'.
- If you get 'a', you have to look for "bb" next to end with.
- If you get 'b', you have to look for the whole pattern "abb" to end with.
Try again. Check here for thes answer.
20. DFA that accepts strings that DO NOT end with abb. Σ = {a, b}
Although you can design a DFA for this directly, an easier way to solve this is to design the DFA for strings ending with "abb" and change flip the final states to non-final states and vice-versa. Check here for the answer.
21. DFA that accepts strings that contains abb. Σ = {a, b}
This should be easier than "ends with abb" problem. This is left as exercise.
22. DFA that accepts strings that does not contain abb. Σ = {a, b}
This is left as exercise.
23. DFA that accepts strings that does not contain two consecutive a's. Σ = {a, b}
This is left as exercise.
24. DFA that accepts strings that starts with two a's and ends with two a's. Σ = {a, b}
This is left as exercise.
