| Prev | Next |
Regular Grammar - NFA Equivalence
In the last section, we saw how regular languages can be specified using regular grammar. The grammar was written in a particular fashion. For instance,
We wrote the grammar for (a+b)(a+b) as S → aA | bA ; A → a | b. This is not the only way to write the grammar. We could write as S → aa | ab | ba | bb which is equally correct.
Similarly, we could have written the grammar for (a+b)*abb as S → aS | bS | abb. But we chose to write it as S → aS | bS | aB ; B → bC ; C → b.
There is a definite advantage with this way of specifying the grammar. This is called as right-linear grammar. It can be easily turned into an NFA. In a right-linear grammar, the right-hand side of a production (or rule) is either a terminal or a terminal followed by a non-terminal.
We will now demonstrate the construction of NFA with few examples.
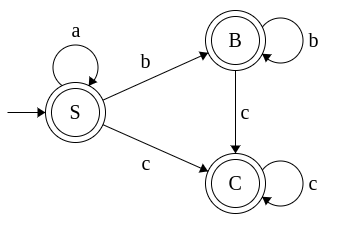
Example 1: The grammar for the regex (a+b)(a+b)
S → aA
S → bA
A → a
A → b
Lets convert the grammar to an equivalent NFA step-by-step.
| Regular grammar | Equivalent NFA |
| S → aA S → bA A → a A → b |
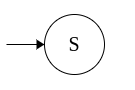
| S → aA S → bA A → a A → b |
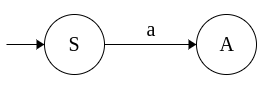
|
| S → aA S → bA A → a A → b |
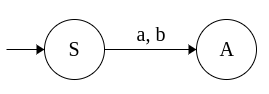
|
| S → aA S → bA A → a A → b |
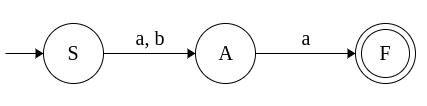
|
| S → aA S → bA A → a A → b |
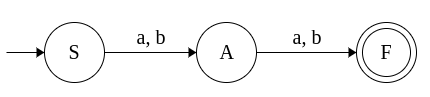
|
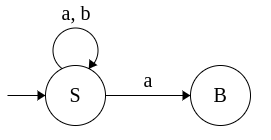
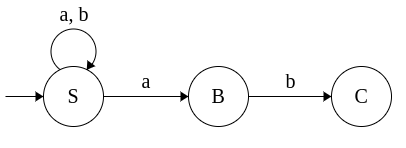
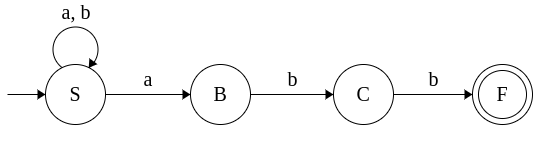
Example 2: Grammar for (a+b)*abb
-
S → aS
S → bS
S → aB
B → bC
C → b
This grammar is converted to equivalent NFA as follows:
| Regular grammar | Equivalent NFA |
| S → aS S → bS S → aB B → bC C → b |
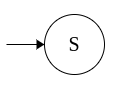 |
| S → aS S → bS S → aB B → bC C → b |
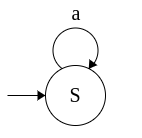 |
| S → aS S → bS S → aB B → bC C → b |
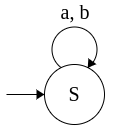 |
| S → aS S → bS S → aB B → bC C → b |
 |
| S → aS S → bS S → aB B → bC C → b |
 |
| S → aS S → bS S → aB B → bC C → b |
 |
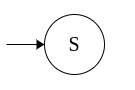
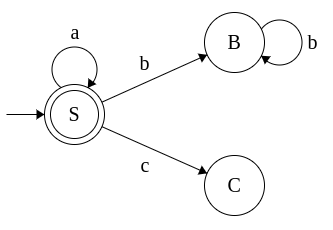
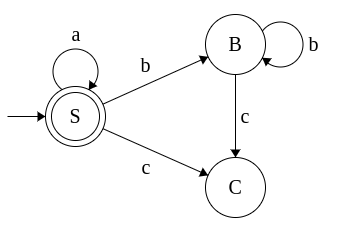
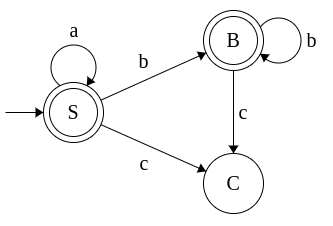
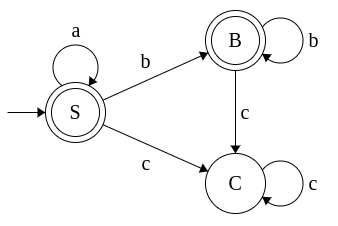
Example 3: Grammar for a*b*c*
-
S → aS
S → bB
S → cC
S → ε
B → bB
B → cC
B → ε
C → cC
C → ε
This grammar is converted to equivalent NFA as follows:
| Regular grammar | Equivalent NFA |
|
S → aS S → bB S → cC S → ε B → bB B → cC B → ε C → cC C → ε |
 |
|
S → aS S → bB S → cC S → ε B → bB B → cC B → ε C → cC C → ε |
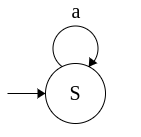 |
|
S → aS S → bB S → cC S → ε B → bB B → cC B → ε C → cC C → ε |
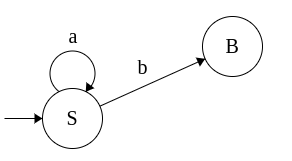 |
|
S → aS S → bB S → cC S → ε B → bB B → cC B → ε C → cC C → ε |
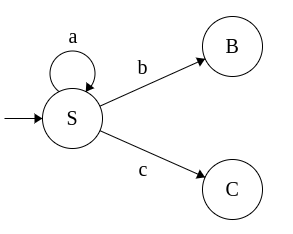 |
|
S → aS S → bB S → cC S → ε B → bB B → cC B → ε C → cC C → ε |
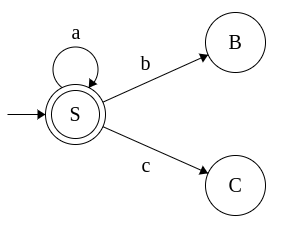 |
|
S → aS S → bB S → cC S → ε B → bB B → cC B → ε C → cC C → ε |
 |
|
S → aS S → bB S → cC S → ε B → bB B → cC B → ε C → cC C → ε |
 |
|
S → aS S → bB S → cC S → ε B → bB B → cC B → ε C → cC C → ε |
 |
|
S → aS S → bB S → cC S → ε B → bB B → cC B → ε C → cC C → ε |
 |
|
S → aS S → bB S → cC S → ε B → bB B → cC B → ε C → cC C → ε |
 |
