| Prev | Next |
DFA Minimization
The DFAs designed for a given problem need not be unique. There can be more than one ways to construct them. For instance, in one of the DFA applications that we saw two ways of constructing DFA to find if a binary string is divisible by 4.
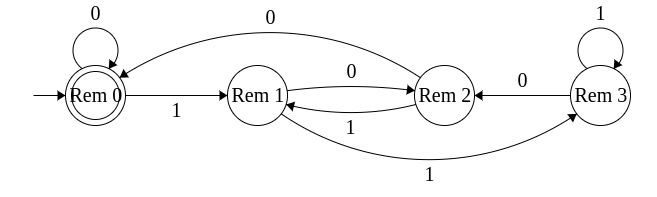
- Approach 1. By maintaining a state for each reminder: 0, 1, 2 and 3. This DFA had 4 states.
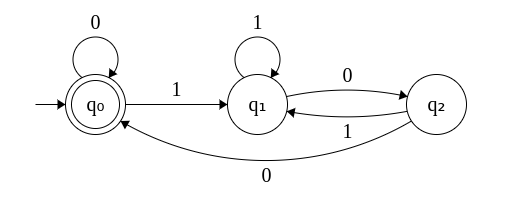
- Approach 2. By constructing DFA to accept binary strings that end with 00. This DFA had 3 states.
Question 1: How can we ascertain that both the DFAs are fundamentally same?
If we can reduce both the DFAs to its minimal size set of states and transitions and show that they are identical, we can indeed prove this fact.
Question 2: Is it possible?
Yes. It is possible. DFA minimization is a key to answering this question.
Question 3: How do we go about it?
If two DFAs accept the same set of strings, but have different number of states (and transitions), it means that the additional states are redundant. Stated otherwise, more than one state is doing the same job and hence they can be merged.
In the above DFA's for divisibility by 4 - one with four states and the other with 3 states - can you recognize which two states do the same job?
- Firstly, there is exactly one final state in each DFA. So they must be identical.
- Now, let's look at Rem 1 and q1. Are they identical?
- Next, we compare Rem 2 and q2. Are they identical?
- In fact, Rem 0 and q0 are indeed identical.
- On input 0, both remain in the same state.
- On input 1, they move to Rem 1 and q1 respectively.
- On input 0, Rem 1 moves to Rem 2 and q0 moves to q1.
- But, on input 1, Rem 1 moves to Rem 3 while q1 stays in the same state.
Apparently different.
- However, on closer examination, we note that Rem 3 remains in the same state on input 1.
- Moreover, Rem 1 and Rem 3 move to Rem 2 on input 0. Behavior on input 0 seems consistent.
- Hence, Rem 1 and Rem 3 are seemingly doing the same job and hence they can be merged.
- Yes. They are identical.
- On input 0, Rem 2 moves to Rem 0 and q2 moves to q0.
- On input 1, Rem 2 moves to Rem 1 and q2 moves to q1.
Hopcroft's Algorithm for DFA minimization
Hopcroft's algorithm is based on Myhill-Nerode equivalence relation that splits the states into a group of equivalent classes. A set of states belong to the same class provided they exhibit the same behavior.
Step 1: To start with, we partition the states into two classes.
- Partition 1 groups all states that are final.
- Partition 2 groups all states that a non-final.
In other words, we hypothesize that all the final states may possibly exhibit same behavior and all non-final states may exhibit same behavior.
Step 2: Next, we check if all the states in the same paritition exhibit the same behavior.
Definition: Two states are said to be exhibiting the same behavior if and only if for each input, both the states makes transitions to the same partition (not necessarily the same state).
If it is not so, the partition needs to be broken down further and the states are reassigned to different partitions according to their behavior.
Step 3: Re-compute the transitions with respect to the modified partition set.
Steps 2 and 3 are repeated until
- Either the states in each partition exhibit consistent behavior or
- The partitions have exactly one state and cannot be broken further
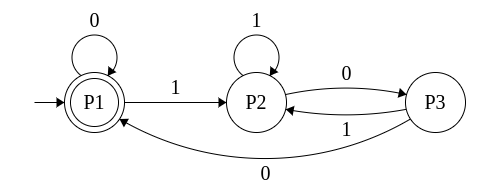
Example: Let us minimize the first DFA of divisibility by 4.
Step 1
| Partition | States | Input 0 | Input 1 |
| P1 | Rem 0 | P1 (Rem 0) | P2 (Rem 1) |
| P2 | Rem 1 Rem 2 Rem 3 |
P2 (Rem 2) P1 (Rem 0) P2 (Rem 2) |
P2 (Rem 3) P2 (Rem 1) P2 (Rem 3) |
Step 2
- Partition P1 has only one state and hence there is no chance of inconsistency in behavior.
- In Partition P2, Rem 1 and Rem 3 show a consistent behavior. However, Rem 2 is not consistent with Rem 1 and Rem 3 for input 0. Hence, Rem 2 needs to be moved to a new partition (say P3).
| Partition | States | Input 0 | Input 1 |
| P1 | Rem 0 | P1 (Rem 0) | P2 (Rem 1) |
| P2 | Rem 1 Rem 3 |
||
| P3 | Rem 2 |
Step 3
- Re-computing the transitions for P2 and P3 we get the following table.
| Partition | States | Input 0 | Input 1 |
| P1 | Rem 0 | P1 (Rem 0) | P2 (Rem 1) |
| P2 | Rem 1 Rem 3 |
P3 (Rem 2) P3 (Rem 2) |
P2 (Rem 3) P2 (Rem 3) |
| P3 | Rem 2 | P1 (Rem 0) | P2 (Rem 1) |
We now note that the states within each partition exhibit consistent behavior and no more partitioning is necessary. The algorithm ends. The minimal DFA can now be drawn as follows.
Exercises
1. Divisibility by 8: Design DFA using reminder method, minimize the DFA and check if it is same as the one ending with 000.
2. Minimize the following DFA.
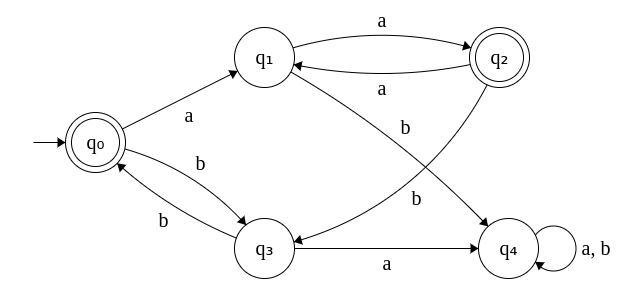
3. Minimize the following DFA.
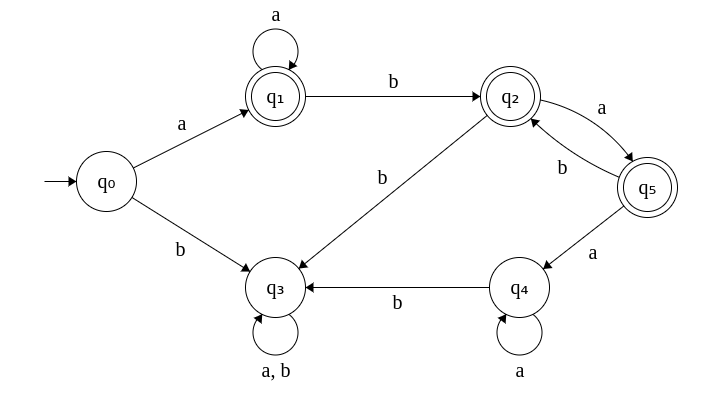
4. Minimize the following DFA.