Prev Next

Pumping lemma and its applications

Not all languages are regular. For example, the language L = {anbn : n ≥ 0} is not regular. Similarly, the language {ap : p is a prime number} is not regular. A pertinent question therefore is how do we know if a language is not regular.

Question: Can we conclude that a language is not regular if no one could come up with a DFA, NFA, ε-NFA, regular expression or regular grammar so far?
 - No. Since, someone may very well come up with any of these in future.

We need a property that just holds for regular languages and so we can prove that any language without that property is not regular. Let's recall some of the properties.

  • We have seen that a regular language can be expressed by a finite state automaton. Be it deterministic or non-deterministic, the automaton consists of a finite set of states.

  • Since the states are finite, if the automaton has no loop, the language would be finite.

    • - Any finite language is indeed a regular language since we can express the language using the regular
      expression: S1 + S2 + ... + SN, where N is the total number of strings accepted by the automaton.

  • However, if the automaton has a loop, it is capable of accepting infinite number of strings.

    • - Because, we can loop around any number of times and keep producing more and more strings.
    - This property is called the pumping property (elaborated below).

The pumping property of regular languages

Any finite automaton with a loop can be divided into parts three.

  • Part 1: The transitions it takes before the loop.
  • Part 2: The transitions it takes during the loop.
  • Part 3: The transitions it takes after the loop.

For example consider the following DFA. It accepts all strings that start with aba followed by any number of baa's and finally ending with ba.

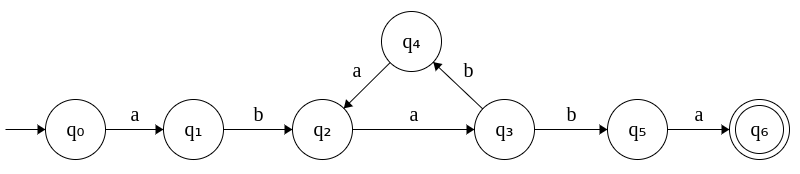
1. What strings are accepted by this DFA?
  ababaaba, ababaabaaba, ababaabaabaaba, .... so on and so forth. Thus the strings accepted by the above DFA can be divided into three parts: aba, (baa)i and ba. Here, i > 0.

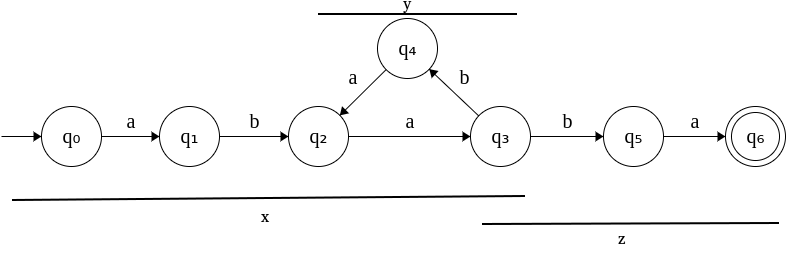
Investigating this further, we can say that any string w accepted by this DFA can be written as w = x yi z
where y represents the part that can be pumped again and again to generate more and more valid strings. This is shown below for the given example.

Before we generalize further, let's investigate this example a little more.

2. What if the loop was at the beginning? Say a self-loop at q0 instead of at q2.
  Then x = ε or |x| = 0. In such a special case, w = yz.

3. What is the loop was at the end. Say a self loop at q6 instead of at q2.
  Then z = ε or |z| = 0. In such a special case, w = xy.

4. Can y be equal to ε ever?
  No. It is impossible. If y = ε, it implies there is no loop which implies the language is finite. We have already seen that a finite language is always regular. So, we are now concerned only with infinite regular language. Hence, y can never be ε. Or |y| > 0.

5. What is the shortest string that is accepted by the DFA?
  ababa. Obviously, a string obtained without going through the loop.
  There is a catch however. See the next question.

6. What is the shortest string accepted if there are more final states? Say q2 is final.
  ab of length 2.

7. What is the longest string accepted by the DFA without going through the loop even once?
  ababa (= xz). So, any string of length > 5 accepted by DFA must go through the loop at least once.

8. What is the longest string accepted by the DFA by going through the loop exactly once?
  ababaaba (= xyz) of length 8. We call this pumping length.

More precisely, pumping length is an integer p denoting the length of the string w such that w is obtained by going through the loop exactly once. In other words, |w| = |xyz| = p.

9. Of what use is this pumping length p?
  We can be sure that |xy| ≤ p. This can be used to prove a language non-regular.

Now, let's define a regular language based on the pumping property.

Pumping Lemma: If L is a regular language, then there exists a constant p such that every string w ∈ L, of length p or more can be written as w = xyz, where

  1. |y| > 0
  2. |xy| ≤ p
  3. xyiz ∈ L for all i

Proving languages non-regular

1. The language L = { anbn : n ≠ 0 } is not regular.

Before proving L is not regular using pumping property, let's see why we can't come up with a DFA or regular expression for L.

L = { ε, ab, aabb, aaabbb, .... }

It may be tempting to use the regular expression a*b* to describe L. No doubt, a*b* generates these strings. However, it is not appropriate since it generates other strings not in L such as a, b, aa, ab, aaa, aab, abb, ...

Let's try to come up with a DFA. Since it has to accept ε, start state has to be final. The following DFA can accept anbn for n ≤ 3. i.e. {ε, a, b, ab, aabb, aaabbb}

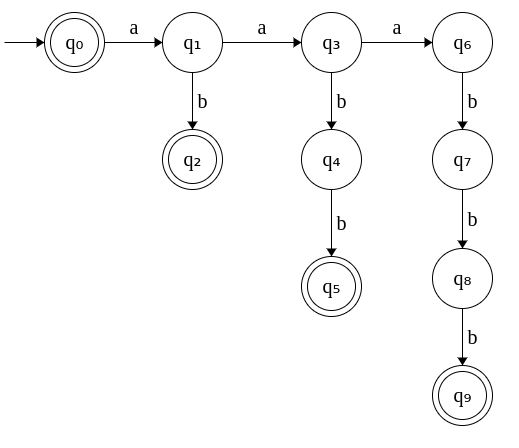
The basic problem is DFA does not have any memory. A transition just depends on the current state. So it cannot keep count of how many a's it has seen. So, it has no way to match the number of a's and b's. So, only way to accept all the strings of L is to keep adding newer and newer states which makes automaton to infinite states since n is unbounded.

Now, let's prove that L does not have the pumping property.

Lets assume L is regular. Let p be the pumping length.

Consider a string w = aa....abb....b such that |w| = p.

    ⇒ w = ap/2bp/2

We know that w can be broken into three terms xyz such that y ≠ ε and xyiz ∈ L.

There are three cases to consider.

  • Case 1: y is made up of only a's

    • Then xy2z has more a's than b's and does not belong to L.

  • Case 2: y is made up of only b's

    • Then xy2z has more b's than a's and does not belong to L.

  • Case 3: y is made up of a's and b's

    • Then xy2z has a's and b's out of order and does not belong to L.

Since none of the 3 cases hold, the pumping property does not hold for L. And therefore L is not regular.

2. The language L = { uuR : u ∈ {a,b}*} is not regular.

Lets assume L is regular. Let p be the pumping length.

Consider a string w = apbbap.

    |w| = 2p + 2 ≥ p

Since, xy ≤ p, xy will consist of only a's.

    ⇒ y is made of only a's
    ⇒ y2 is made of more number of a's than y since |y| > 0
      (Let's say y2 has m a's more than y where m > 1)
    ⇒ xy2z = ap+mbbap where m ≥ 1
    ⇒ xy2z = ap+mbbap cannot belong to L.

Therefore, pumping property does not hold for L. Hence, L is not regular.

3. The language L = { an : n is prime } is not regular.

Lets assume L is regular. Let p be the pumping length. Let q ≥ p be a prime number (since we cannot assume that pumping length p will be prime).

Consider the string w = aa....a such that |w| = q ≥ p.

We know that w can be broken into three terms xyz such that y ≠ ε and xyiz ∈ L

    ⇒ xyq+1z must belong to L
    ⇒ |xyq+1z| must be prime
    |xyq+1z| = |xyzyq|
          = |xyz| + |yq|
          = q + q.|y|
          = q(1 + |y|) which is a composite number.

Therefore, xyq+1z cannot belong to L. Hence, L is not regular.

Exercises

Show that the following languages are not regular.

4. L = { anbm : n ≠ m }

5. L = { anbm : n > m }

6. L = { w : na(w) = nb(w) }

7. L = { ww : w ∈ {a,b}* }

8. L = { an2 : n > 0 }

IMPORTANT NOTE

Never use pumping lemma to prove a language regular. Pumping property is necessary but not sufficient for regularity.