Formal Languages and Automata

Prev

Next

Non-deterministic Finite State Automata

Designing a DFA can turn out to be a little tricky in certain cases (as you would have observed in a few problems). DFA has to be carefully designed since we should accept only strings that are to be accepted. No more or no less. The difficulty is due to the restriction that, from each state we can make a transition to exactly one state for each input symbol. Non-determinstic Finite state Automata (NFA) removes this restriction and thereby simplifying the design.

We will first show how to construct an NFA, step-by-step, with an example. We will later show the equivalence of NFA and DFA. i.e. Every NFA can be turned into a DFA in an algorithmic fashion.

A non-deterministic finite state automaton is a 5-tuple (Q, Σ, δ, q₀, F) where

• Q denotes the finite set of states
• Σ represents the alphabet that consists of input symbols
• δ: Q x Σ = Q denotes the transition function the defines the transition from q_i ∈ Q to {q_j ∈, ..., q_k} Q for each input symbol.
• q₀ denotes the start state
• F denotes the set of final states

Given an input sequence, the NFA processes the string of symbols one at a time, moves between the states in a non-determinstic fashion, as defined by the transition function δ. The string is said to be accepted by the NFA, if at the end of the processing, a final state is reached.

Let's do some examples.

1. NFA that accepts strings that end with abb. Σ = {a, b}

This can be done in a straight-forward fashion as shown below. Read any number of a's and b's and remain in q₀ until you "abb" at the end.

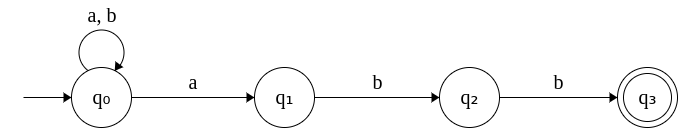
As an example, consider the string: aaaaabb. i.e. Five a's followed by two b's. The NFA remains in q₀ while reading the first four a's. When it reads the fifth a, it jumps to q₁.

δ(q₀,aaaaabb) → δ({q₀,q₁},aaaabb) → δ({q₀,q₁},aaabb) → δ({q₀,q₁},aabb) → δ({q₀,q₁},abb) → δ({q₀,q₁},bb) → δ({q₀,q₂},b) →{q₀,q₃}

How does the NFA "magically" know ahead which transition to make?

It doesn't have to. All it does is, it makes both transitions by maintaining a set of states it could possibly be in, as it reads and processes the input string. After the entire string is read, if at least one of the states in the set is final, the input string is accepted. If none of the states are final, the input string is rejected.

Note that there are two transitions possible from q₀ for the input symbol 'a' in the above example. i.e. δ(q₀,a) = {q₀, q₁}. In other words, a transition in an NFA is a movement from one state to a set of states.

Contrast this with the DFA directly constructed (shown below for convenience)

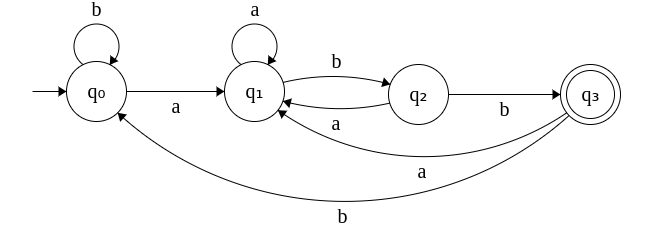
You can observe that the NFA is far simpler to construct than the original DFA. It doesn't however imply, NFA is more powerful compared to DFA. i.e. if a NFA can be designed for a problem, it can easily be converted to an equivalent DFA.

2. NFA that accepts strings that contains abb. Σ = {a, b}

This is left as exercise.

3. NFA that accepts strings that does not contain abb. Σ = {a, b}

This is left as exercise.

4. NFA that accepts strings that starts with two a's and ends with two a's. Σ = {a, b}

Try on your own first. Check here for the NFA.

5. NFA that accepts strings that end with "ab" or "ba". Σ = {a, b}

This is left as exercise.

6. NFA that accepts strings that starts and ends with different symbols Σ = {a, b}

This is left as an exercise.

ε-Non deterministic Finite Automata

ε-NFA is a form of NFA that allows a greater degree of freedom in its construction. More specifically, it allows for ε-transitions. i.e. the NFA can move to another state without having to read a symbol (or by reading an ε.

Of what use is this "extra" freedom?

This freedom is valuable when we have to combine multiple NFAs into one. For example, consider problems 4 and 5 above. Both of them can be broken down into two subproblems. It makes sense to design separate NFAs for the subproblems and combine them. We will demonstrate this for problem 4. Let's call this problem 4A.

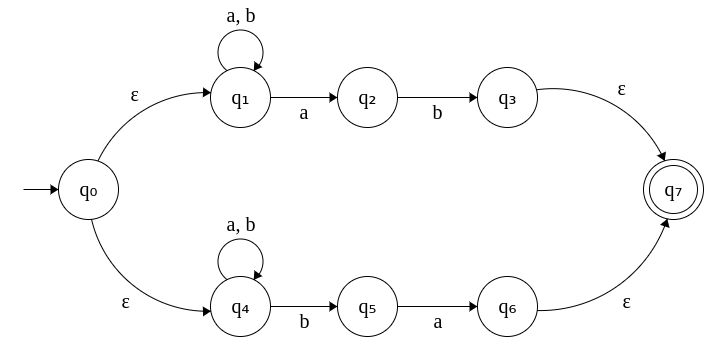
4A. ε-NFA that accepts strings that end with "ab" or "ba". Σ = {a, b}

Subproblem 1. The NFA that accepts strings ending with "ab" is given by

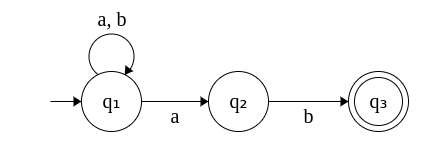
Subproblem 2. The NFA that accepts strings ending with "ba" is given by

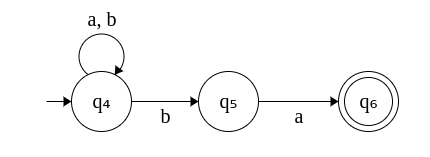
These two machines can be combined as follows:

• Add a new start state q₀, with two epsilon transitions to the start states of the two NFAs q₁ and q₄. Now q₀ is the new start state of the combined ε-NFA.


• Add a new final state q₇, with two epsilon transtions from the final states of the two NFAs q₃ and q₆. Now q₇ is the new final state of the combined ε-NFA.